Energy Losses in Pharmaceutical Engineering: The change in velocity of the fluid in a flow (either in magnitude or direction) induces large-scale turbulence due to the formation of eddies. So, a portion of energy possessed by the flowing fluid is ultimately dissipated as heat by radiation and is considered to be the loss of energy. Some of the reasons for loss of energy caused by the change in velocity are sudden pipe enlargement, sudden contraction, entrance to a pipe from a large vessel, exit from a pipe, obstruction in the flow passage, gradual contraction or enlargement, bends, and various pipe fittings, etc. These losses of energy are termed as ‘minor’ losses because the magnitude of these losses is quite small compared to the loss due to friction in long pipes which are distinguished as ‘major losses’. The ‘minor losses’ are confined to a very short length of the passage of the flowing liquid. The analytical expressions representing the loss of energy for the above cases are discussed below.
Energy Loss by Sudden Enlargement
Table of Contents
Consider a pipe of cross-sectional area A1 carrying a liquid of specific weight w. It is connected to another pipe of larger cross-sectional area A2. As there is a sudden increase in the cross-sectional area of flow passage the liquid released from a smaller pipe is unable to follow the abrupt change in boundary, Fig.1.
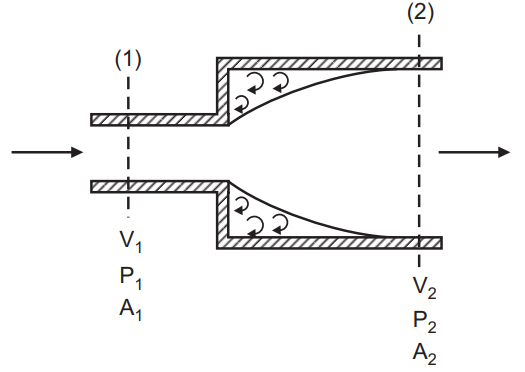
Consequently, the flow separates from the boundary, forming turbulent eddies that result in the loss of energy dissipated as heat by radiation. If P1, V1, and P2, V2 are the pressures and velocities of the flow of liquid in the narrower and wider pipe, respectively, then by continuity equation, the discharge (Q) is,
Q = A1V1 = A2V2…..(1)
The force acting on the liquid in the controlled volume in the direction of flow is expressed as
P1A1 + P1 (A2 – A1) – P2A2 = (P1 – P2) A2…..(2)
Using Newton’s second law for the rate of change of momentum and the head loss between two sections ‘1′ and ‘2′ due to sudden enlargement, upon applying Bernoulli’s equation we get
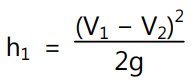
Using continuity equation, equation (3) may be expressed as,
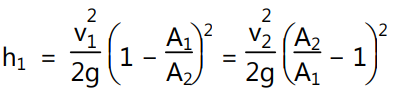
Equations (3) and (4) is the expression for head loss due to sudden enlargement.
Energy Loss by Sudden Contraction
Consider a pipe carrying a certain liquid of specific weight w whose cross-sectional area at a certain section reduces abruptly from A1 to A2 as shown in Fig.2. A sudden contraction in the geometry of pipe leads to streamlines between section ‘1′ and ‘2′ curved and the liquid is accelerated. Thus, pressure at the annular face varies in an unknown manner and it cannot be determined. There is no major loss of energy in the region between section 1 and the accelerating flow in the converging part.
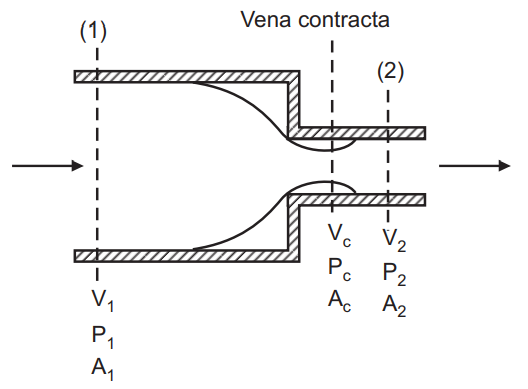
As the liquid flows from the wider pipe to the narrower pipe, a vena-contract is formed and is followed by further widening of the liquid stream to fill up completely the narrower pipe. In between the vena contract and the wall of the pipe, a lot of eddies have formed that account for considerable dissipation of energy. In this region, the flow pattern is almost similar to that of sudden enlargement.
In general, the loss of head due to sudden contraction is expressed as:
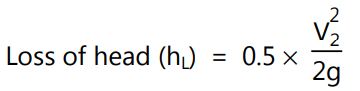
Energy Loss at Pipe Entrance
Energy loss at the entrance to the pipe is also called ‘inlet loss’. It occurs when the liquid enters the pipe from a large vessel (or tank). The flow pattern is similar to that of sudden contraction. In general, for a sharp-cornered entrance, the loss of head at the entrance is expressed as :
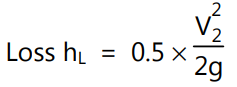
where V2 is the mean velocity of flow of liquid in the pipe.
Energy Loss at Pipe Exit
The outlet end of a pipe carrying liquid may be either left free or connected to a large reservoir. The liquid leaving the pipe possesses some kinetic energy corresponding to the velocity of the flow in the pipe which is ultimately dissipated either in the form of free jet or turbulence in the reservoir depending on the outlet condition in the pipe. The loss may be determined by using Eq. (6) with the conditions for which A2 → ∞. So, the loss of head at the exit of the pipe expressed as
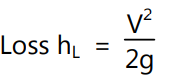
where V is the mean velocity of flow of liquid in the pipe.
Energy Loss by Obstruction in Flow Passage
The loss of energy due to flow obstruction in a pipe occurs due to the sudden reduction in the cross-sectional area followed by an abrupt enlargement of the stream beyond the obstruction, Fig.3.
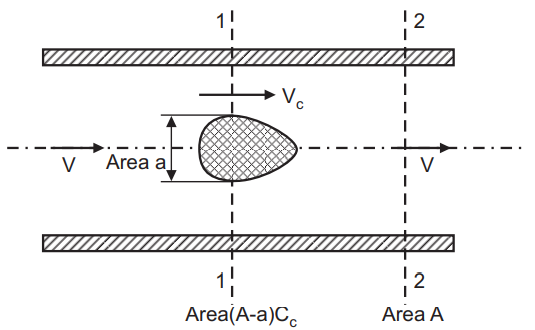
Consider a pipe flow (cross-sectional area of the pipe is A) in which obstruction is placed with maximum cross-sectional area ‘a’. As the flow passage is reduced to (A − a), a vena-contracta is formed beyond which the flow becomes uniform after a certain distance from vena-contracta. If Vc and V be the velocities at vena-contracta and at the section where the flow is uniform, then the loss of head due to obstruction can be deduced as
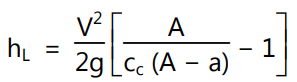
Make sure you also check our other amazing Article on : Reynolds Number and Its Significance
