Kruskal-Wallis Test: The Kruskal-Wallis ‘H’ test is a rank-based nonparametric test used to compare outcomes among more than two independent groups. This test is also called one-way ANOVA on ranks. The parametric equivalent of the Kruskal-Wallis test is the one-way analysis of variance (ANOVA). This test ranks of the data values are used in place of the actual data points. It is used for comparing two or more independent samples of equal or different sample sizes. The test determines whether the medians of two or more groups are different Kruskal-Wallis test is an alternative to one-way ANOVA when the data violates the assumptions of normal distribution and when the sample size is too small. It can be used for both continuous and ordinal dependent variables. It extends the Mann-Whitney U test which is used for the comparison of two groups. The p-value for both the Kruskal Wallis and the Mann-Whitney test are equal. The assumptions of the Kruskal Wallis test are as follows:
- There should not be any relationship between the members in each group or between groups (independent).
- Variables should contain one independent variable with two or more levels (independent groups).
- Dependent variables must be measured at the ordinal scale, ratio scale, or interval scale.
- All groups should have the same shape distributions.
The test statistic used in the Kruskal-Wallis test is called the ‘H’ statistic. The hypothesis for the test are:
Null hypothesis: Ho: Population medians are equal.
Alternative hypothesis: H1: Population medians are not equal.
The test statistic for the Kruskal-Wallis test is approximately distributed as Chi-square with K – 1 degree of freedom. In H-test, the degree of freedom is determined by the following formula:
where,
- df = K -1
- df = Degrees of freedom
- K = Number of groups or samples
In Kruskal-Wallis H-test, the first step is to combine all the samples and perform a rank ordering on all the values. The Kruskal-Wallis H-test value is calculated by using the following formula.
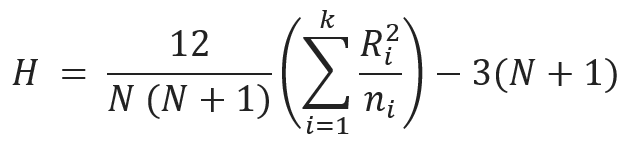
where,
- N = Total number of observations in all grouped samples
- K = Number of comparison groups
- Ri = Sum of the ranks in the first group
- ni = Sample size in the first group
If the p-value is less than 5% or greater than 10%, then reject the null hypothesis and if the p-value is between 5% and 10% then accept the null hypothesis.
For example, patients suffering from dengue are divided into three groups and three different types of treatment are given to them. The platelet count of all patients are measured after 3-day course of treatment and results are as follows:
Treatment 1: 49,000, 41,000, 45,000, 58,000, 65,000
Treatment 2: 58,000, 62,000, 78,000
Treatment 3: 62,000, 75,000, 79,000, 84,000
The sample size is different for the three treatments.
Treatment 1: n1 = 5
Treatment 2: n₂ = 3
Treatment 3: n3 = 4
Total sample size (N) = n₁ +n₂ + n3 = 5+3+4 = 12.
Order these samples from smallest to largest and then assign ranks to the clubbed sample.
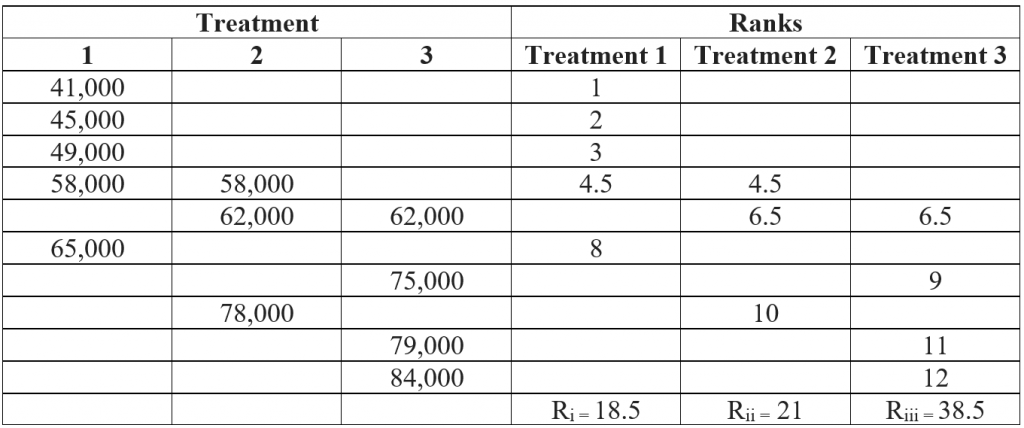
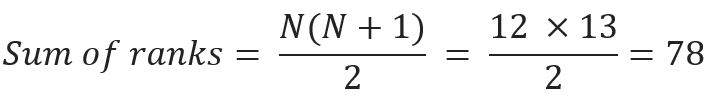
Here the sum of ranks = 78.
Here, we have to check that there is a difference between the 3 population medians so we have to summarise the sample information in test statistic (H) on ranks.

Determine the critical value of H using the table of critical values and the critical value is 5.656. The criteria for rejection or acceptance of null hypothesis is as follows:
Reject Ho : H > Critical value
Accept Ho : H < Critical value
Here, we reject the null hypothesis because the H value is greater than the critical value and the conclusion is “there is no significant evidence to state that the three population medians are same.
Make sure you also check our other amazing Article on : Difference Between Type 1 and Type 2 Errors