Redox Titration

Redox Titration: Analytical titrations using redox reactions were introduced shortly after the development of acid-base titrimetry. The earliest redox titration took advantage of the oxidizing power of chlorine. 

In 1787, Claude Berthollet introduced a method for the quantitative analysis of chlorine water (a mixture of Cl₂, HCl, and HOCl) based on its ability to oxidize indigo, a dye that is colorless in its oxidized state. 

In 1814, Joseph Gay-Lussac developed a similar method for determining chlorine in bleaching powder. In both methods, the endpoint is a color change. Before the equivalence point, the solution is colorless due to the oxidation of indigo. After the equivalence point, however, unreacted indigo imparts a permanent color to the solution. 

The number of redox titrimetric methods increased in the mid-1800s with the introduction of MnO₄⁻, Cr₂O₇²⁻, and I₂ as oxidizing titrants, and of Fe²⁺ and S₂O₃²⁻   as reducing titrants. 

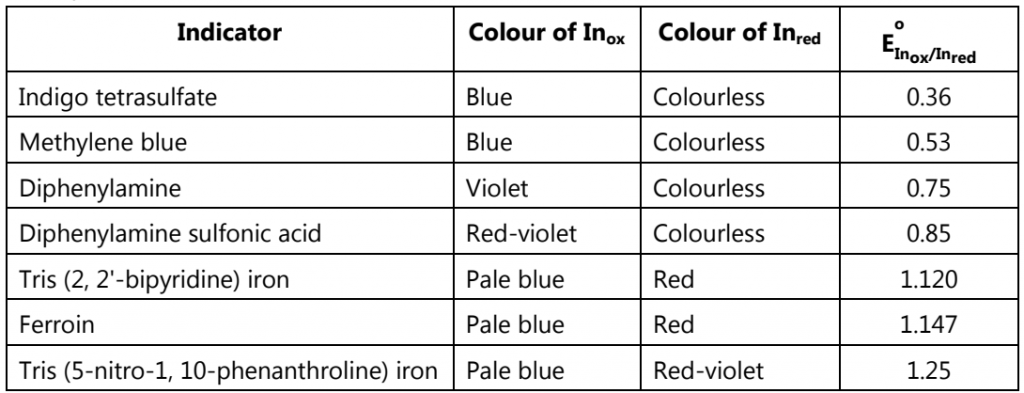
A titrant can serve as an indicator if its oxidized and reduced forms differ significantly in color. For example, the intensely purple MnO₄⁻ ion serves as its indicator since its reduced form, Mn²⁺, is almost colorless. 

Other titrants require a separate indicator. The first such indicator, diphenylamine, was introduced in 1920. Other redox indicators soon followed, increasing the applicability of redox titrimetry.

Redox Titration Curve 

To evaluate a redox titration we need to know the shape of its titration curve. In an acid-base titration or a complexation titration, the titration curve shows how the concentration of H₃O⁺ (as pH) or Mⁿ⁺ (as pM) changes as we add titrant. 

For redox titration, it is convenient to monitor the titration reaction’s potential instead of the concentration of one species. 

The Nernst equation relates a solution’s potential to the concentrations of reactants and products participating in the redox reaction.

Consider, for example, titration in which a titrand in a reduced state, A_red, reacts with a titrant in an oxidized state, B_ox. 

A_red + B_ox ↔ B_red + A_ox

where A_ox is the titrant’s oxidized form, and Bred is the titrant’s reduced form.  The reaction’s potential, E_rxn, is the difference between the reduction potentials for each half-reaction. 

E _rxn = E B_ox/B_red − E A_ox/A_red

After each addition of titrant, the reaction between the titrand and the titrant reaches a state of equilibrium. Because the potential at equilibrium is zero, the titrant’s and the titrant’s reduction potentials are identical. 

E B_ox/B_red = E A_ox/A_red

This is an important observation because we can use either half-reaction to monitor the titration’s progress. 

Before the equivalence point, the titration mixture consists of appreciable quantities of the titrand’s oxidized and reduced forms. The concentration of unreacted titrant, however, is very small. The potential, therefore, is easier to calculate if we use the Nernst equation for the titrand’s half-reaction. 

E_rxn = E_o A_ox/A_red − RTnF ln [A_red] [A_ox]

Although the Nernst equation is written in terms of the half-reaction’s standard state potential, a matrix-dependent formal potential often is used in its place. 

After the equivalence point, it is easier to calculate the potential using the Nernst equation for the titrant’s half-reaction. 

E_rxn = EoB_ox/B_red − RTnF ln [B_red] [B_ox]

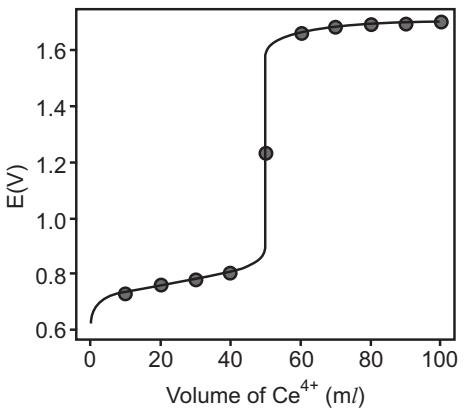
Sketching of Redox Titration Curve 

Let us use the titration of 50.0 ml of 0.100 M Fe²⁺ with 0.100 M Ce⁴⁺ in a matrix of 1M HClO₄. 

We begin by calculating the titration’s equivalence point volume, which, as we determined earlier, is 50.0 ml. Next, we draw our axes, placing the potential, E, on the y-axis and the titrant’s volume on the x-axis. To indicate the equivalence point’s volume, we draw a vertical line corresponding to 50.0 ml of Ce⁴⁺. Fig.1 shows the result of the first step in our sketch. 

Before the equivalence point, the potential is determined by a redox buffer of Fe²⁺ and Fe³⁺. Although we can easily calculate the potential using the Nernst equation, we can avoid this calculation by making a simple assumption. A redox buffer operates over a range of potentials that extends approximately ± (0.05916/n) unit on either side of E^o_Fe ³⁺ /Fe²⁺. The potential is at the buffer’s lower limit 

E = E^o_Fe³⁺ /Fe²⁺ (−0.05916) 

when the concentration of Fe²⁺ is 10 × greater than that of Fe³⁺. The buffer reaches its upper potential 

E = E_Fe^{o 3+} /_Fe²⁺ ( 0.05916) 

When the concentration of Fe²⁺ is 10 × smaller than that of Fe³⁺. The redox buffer spans a range of volumes from approximately 10% of the equivalence point volume to approximately 90% of the equivalence point volume. 

The next step in sketching our titration curve is to add two points after the equivalence point. Here the potential is controlled by a redox buffer of Ce³⁺ and Ce⁴⁺. The redox buffer is at its lower limit of E = E_Ce^o4+ /Ce³⁺ – 0.05916 when the titrant reaches 110% of the equivalence point volume and the potential is E_Ce^o4+ /Ce³⁺  when the volume of Ce⁴⁺ is 2 × V_eq. 

Finding End Point with Indicator 

Three types of indicators are used to signal a redox titration’s endpoint. The oxidized and reduced forms of some titrants, such as MnO₄⁻, have different colors. A solution of MnO₄⁻   is intensely purple. 

In an acidic solution, however, permanganate’s reduced form, Mn²⁺, is nearly colorless.  When using MnO₄⁻   as a titrant, the titrand’s solution remains colorless until the equivalence point. The first drop of excess MnO₄⁻ produces a permanent tinge of purple, signaling the endpoint. 

Some indicators form a colored compound with a specific oxidized or reduced form of the titrant or the titrand. Starch, for example, forms a dark blue complex with I₃⁻. We can use this distinct color to signal the presence of excess I₃⁻ as a titrant-a change in color from colorless to blue or the completion of a reaction consuming I₃⁻ as the titrand-a change in color from blue to colorless. Another example of a specific indicator is thiocyanate, SCN^–, which forms a soluble red-colored complex of Fe(SCN)²⁺  with Fe³⁺.

The most important class of indicators are substances that do not participate in the redox titration, but whose oxidized and reduced forms differ in color. When we add a redox indicator to the titrand, the indicator imparts a color that depends on the solution’s potential. As the solution’s potential changes with the addition of titrant, the indicator changes oxidation state and changes color, signaling the endpoint. 

To understand the relationship between potential and an indicator’s color, consider its reduction half-reaction. 

In_ox + ne⁻ ↔ In_red

where In_ox and In_red are, respectively, the indicator’s oxidized and reduced forms.  A partial list of redox indicators is shown in the table below:

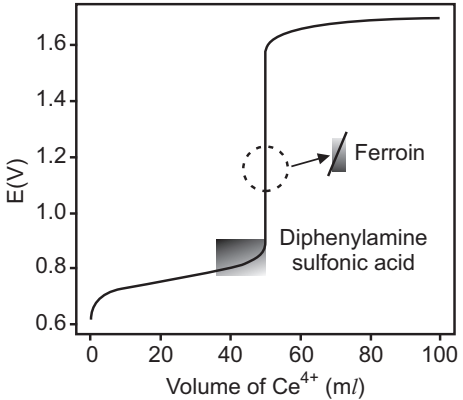
The endpoint transitions for the indicators diphenylamine sulfonic acid and ferroin are superimposed on the titration curve. Because the transition for ferroin is too small to see on the scale of the x-axis, it requires only 1–2 drops of titrant − the color change is expanded to the right.

Other Methods for End Point Detection 

Another method for locating a redox titration’s endpoint is a potentiometric titration in which we monitor the change in potential while adding the titrant to the titrand. The endpoint is found by visually examining the titration curve. The simplest experimental design for a potentiometric titration consists of a platinum indicator electrode whose potential is governed by the titrand’s or titrant’s redox half-reaction, and a reference electrode that has a fixed potential. 

Other methods for locating the titration’s endpoint include thermometric titrations and spectrophotometric titrations. 

Quantitative Applications 

Although many quantitative applications of redox titrimetry have been replaced by other analytical methods, a few important applications continue to be relevant. In this section, we review the general application of redox titrimetry with an emphasis on environmental, pharmaceutical, and industrial applications. 

Adjusting the Titrand’s Oxidation State 

If a redox titration is to be used in quantitative analysis, the titrand must initially be present in a single oxidation state. For example, iron can be determined by a redox titration in which Ce⁴⁺ oxidizes Fe²⁺ to Fe³⁺. Depending on the sample and the method of sample preparation, iron may initially be present in both the +2 and +3 oxidation states. Before titrating, we must reduce any Fe³⁺ to Fe²⁺. This type of pretreatment can be accomplished using an auxiliary reducing agent or oxidizing agent. 

A metal that is easy to oxidize such as Zn, Al, and Ag – can serve as an auxiliary reducing agent. The metal, as a coiled wire or powder, is added to the sample where it reduces the titrand. Because any unreacted auxiliary reducing agent will react with the titrant, it must be removed before beginning the titration. This can be accomplished by simply removing the coiled wire, or by filtering. 

An alternative method for using an auxiliary reducing agent is to immobilize it in a column. To prepare a reduction column an aqueous slurry of the finely divided metal is packed in a glass tube equipped with a porous plug at the bottom. The sample is placed at the top of the column and moves through the column under the influence of gravity or vacuum suction. The length of the reduction column and the flow rate are selected to ensure the analyte’s complete reduction. 

Two common reduction columns are used. In the Jones reductor the column is filled with amalgamated zinc, Zn(Hg), prepared by briefly placing Zn granules in a solution of  HgCl₂. Oxidation of zinc provides the electrons for reducing the titrand. 

Zn(Hg)(s) → Zn²⁺  (aq) + Hg(l) + 2e⁻

In the Walden reductor, the column is filled with granular Ag metal. The solution containing the titrand is acidified with HCl and passed through the column where the oxidation of silver provides the necessary electrons for reducing the titrand. 

Ag(s) + Cl⁻ (aq) → AgCl(s) + e⁻ 

Several reagents are commonly used as auxiliary oxidizing agents, including ammonium peroxy disulfate, (NH₄)₂S₂O₈, and hydrogen peroxide, H₂O₂. Peroxy disulfate is a powerful oxidizing agent. 

S₂O₂ − 8(aq) + 2e⁻ → 2SO₂ − 4(aq) 

capable of oxidizing Mn²⁺ to MnO₄⁻, Cr³⁺ to Cr₂O₇²⁻, and Ce³⁺ to Ce⁴⁺. Excess peroxydisulfate is easily destroyed by briefly boiling the solution. The reduction of hydrogen peroxide in acidic solution

H₂O₂(aq) + 2H + (aq) + 2e⁻ → 2H₂O(l) 

provides another method for oxidizing a titrand. Excess H₂O₂ is destroyed by briefly boiling the solution. 

Selecting and Standardizing a Titrant 

If it is to be used quantitatively, the titrant’s concentration must remain stable during the analysis. Because a titrant in a reduced state is susceptible to air oxidation, most redox titrations use an oxidizing agent as the titrant. There are several common oxidizing titrants, including MnO₄⁻, Cr⁴⁺ to Cr₂O₇²⁻, and I₃⁻. Which titrant is used often depends on how easy it is to oxidize the titrand. A titrand that is a weak reducing agent needs a strong oxidizing titrant if the titration reaction is to have a suitable endpoint. 

The two strongest oxidizing titrants are MnO₄⁻ and Ce⁴⁺, for which the reduction half-reactions are 

MnO₄⁻ (aq) + 8H⁺ (aq) + 5e⁻ ↔ Mn²⁺ (aq) + 4H₂O(l) 

Ce⁴⁺ (aq) + e⁻ ↔ Ce³⁺ (aq) 

Solutions of Ce⁴⁺ usually are prepared from the primary standard cerium ammonium nitrate, Ce(NO₃)₄2NH₄NO₃, in 1 M H₂SO₄. When prepared using a reagent grade material, such as Ce(OH)₄, the solution is standardized against a primary standard reducing agent such as Na₂C₂O₄ or Fe²⁺  (prepared using iron wire) using ferroin as an indicator. Despite its availability as a primary standard and its ease of preparation, Ce⁴⁺ is not as frequently used as MnO₄⁻ because it is more expensive. 

The standardization reactions are 

Ce⁴⁺ (aq) + Fe²⁺ (aq) → Ce³⁺ (aq) + Fe³⁺ (aq) 

2Ce⁴⁺ (aq) + H₂C₂O₄(aq) → 2Ce³⁺ (aq) + 2CO₂(g) + 2H⁺ (aq)

Solutions of MnO₄⁻   are prepared from KMnO₄, which is not available as a primary standard. Aqueous solutions of permanganate are thermodynamically unstable due to its ability to oxidize water. 

4MnO₄⁻ (aq) + 2H₂O(l) ↔ 4MnO₂(s) + 3O₂(g) + 4OH⁻(aq) 

This reaction is catalyzed by the presence of MnO₂, Mn²⁺, heat, light, and the presence of acids and bases. A moderately stable solution of permanganate can be prepared by boiling it for an hour and filtering it through a sintered glass filter to remove any solid MnO₂ that precipitates. Standardization is accomplished against a primary standard reducing agent such as Na₂C₂O₄ or Fe²⁺ (prepared using iron wire), with the pink color of excess MnO₄⁻ signaling the endpoint. A solution of MnO₄⁻ prepared in this fashion is stable for 1–2 weeks, although the standardization should be rechecked periodically. 

The standardization reactions are 

MnO₄⁻ (aq) + 5Fe²⁺ (aq) + 8H⁺ (aq) → Mn²⁺ (aq) + 5Fe³⁺ (aq) + 4H₂O(l) 

2MnO₄⁻ (aq) +5H₂C₂O₄ (aq) + 6H⁺ (aq) → 2Mn²⁺ (aq) + 10CO₂(g) + 8H₂O(l) 

Potassium dichromate is a relatively strong oxidizing agent whose principal advantages are its availability as a primary standard and the long term stability of its solutions. It is not, however, as strong an oxidizing agent as MnO₄⁻ or Ce⁴⁺, which makes it less useful when the titrand is a weak reducing agent. Its reduction half-reaction is 

Cr₂O₇²⁻ (aq) + 14H⁺ (aq) + 6e⁻ → 2Cr³⁺ (aq) + 7H₂O(l) 

Although a solution of Cr₂O₇²⁻ is orange and a solution of Cr³⁺ is green, neither colour is intense enough to serve as a useful indicator. Diphenylamine sulfonic acid, whose oxidized form is red-violet and reduced form is colourless, gives a very distinct end point signal with Cr₂O₇²⁻. 

Iodine is another important oxidizing titrant. Because it is a weaker oxidizing agent than MnO₄⁻, Ce⁴⁺, and Cr₂O₇²⁻, it is useful only when the titrand is a stronger reducing agent. This apparent limitation, however, makes I₂ a more selective titrant for the analysis of a strong reducing agent in the presence of a weaker reducing agent. The reduction half-reaction for I₂ is 

I₂(aq) + 2e⁻ ↔ 2I⁻ (aq) 

Because iodine is not very soluble in water, solutions are prepared by adding an excess of I^–. The complexation reaction 

I₂ (aq) + I⁻ (aq) ↔ I₃⁻ (aq)

increases the solubility of I₂ by forming the more soluble triiodide ion, I₃⁻. Even though iodine is present as I₃⁻ instead of I₂, the number of electrons in the reduction half-reaction is unaffected. 

I₃⁻ (aq) + 2e⁻ ↔3I⁻ (aq) 

Solutions of I₃⁻ are normally standardized against Na₂S₂O₃ using starch as a specific indicator for I₃⁻. 

The standardization reaction is 

I₃⁻ (aq) + 2S₂O₃²⁻ (aq) → 3I⁻ (aq) + 2S₄O₆²⁻ (aq) 

An oxidizing titrant such as MnO₄⁻, Ce⁴⁺, Cr₂O₇^2–, and I₃⁻, is used when the titrand is in a reduced state. If the titrand is in an oxidized state, we can first reduce it with an auxiliary reducing agent and then complete the titration using an oxidizing titrant. Alternatively, we can titrate it using a reducing titrant. Iodide is a relatively strong reducing agent that could serve as a reducing titrant except that a solution of I− is susceptible to the air-oxidation of I^– to I₃⁻. 

3I⁻ (aq) ↔ I₃⁻ (aq) + 2e⁻ 

A freshly prepared solution of KI is clear, but after a few days it may show a faint yellow coloring due to the presence of I₃⁻. 

Instead, adding an excess of KI reduces the titrand, releasing a stoichiometric amount of I₃⁻. The amount of I₃⁻produced is then determined by a back titration using thiosulfate, S₂O₃²⁻, as a reducing titrant. 

2S₂O₃²⁻ (aq) ↔ 2 S₄O₆²⁻ (aq) + 2e⁻ 

Solutions of S₂O₃²⁻ are prepared using Na₂S₂O₃ · 5H₂O, and must be standardized before use. 

Standardization is accomplished by dissolving a carefully weighed portion of the primary standard KIO3 in an acidic solution containing an excess of KI. The reaction between IO₃⁻ and I^–  

IO₃⁻ (aq) + 8I⁻ (aq) + 6H⁺ (aq) → 3I₃⁻ (aq) + 3H₂O(l) 

liberates a stoichiometric amount of I₃⁻. By titrating this I₃⁻ with thiosulfate, using starch as a visual indicator, we can determine the concentration of S₂O₃²⁻ in the titrant. 

The standardization titration is 

I₃⁻ (aq) + 2 S₂O₃²⁻ (aq) → 3I⁻ (aq) + 2 S₄O₆²⁻ (aq) 

which is the same reaction used to standardize solutions of I₃⁻.

Although thiosulfate is one of the few reducing titrants that is not readily oxidized by contact with air, it is subject to slow decomposition of bisulfite and elemental sulfur. If used over several weeks, a solution of thiosulfate should be restandardized periodically. Several forms of bacteria can metabolize thiosulfate, which can also lead to a change in its concentration. This problem can be minimized by adding a preservative such as HgI₂ to the solution. 

Another useful reducing titrant is ferrous ammonium sulfate, Fe(NH₄)2(SO₄)₂· 6H₂O, in which iron is present in the  +2 oxidation state. A solution of Fe²⁺ is susceptible to air oxidation, but when prepared in 0.5 M H₂SO₄ it remains stable for as long as a month.  Periodic restandardization with K₂Cr₂O₇ is advisable. The titrant can be used to directly titrate the titrand by oxidizing Fe²⁺ to Fe³⁺. Alternatively, ferrous ammonium sulfate is added to the titrand in excess and the quantity of Fe³⁺ produced is determined by back titrating with a standard solution of Ce⁴⁺ or Cr₂O₇²⁺.   

Iodometry 

Iodometry is one of the most important redox titration methods. Iodine reacts directly, fast, and quantitively with many organic and inorganic substances. Thanks to its relatively low, pH-independent redox potential, and reversibility of the iodine/iodide reaction, iodometry can be used both to determine the amount of reducing agents (by direct titration with iodine) and of oxidizing agents (by titration of iodine with thiosulfate). In all cases, the same simple and reliable method of endpoint detection, based on the blue starch complex, can be used.  The reversible iodine/iodide reaction mentioned above is 

2I⁻ ↔ I₂ + 2e⁻

and obviously, whether it should be treated as oxidation with iodine or reduction with iodides depends on the other redox system involved. 

The second important reaction used in iodometry is the reduction of iodine with thiosulfate: 

2S₂O₃²⁻ + I₂ → S₂O₃²⁻ + 2I⁻

In the case of both reactions, it is better to avoid low pH. Thiosulfate is unstable in the presence of acids, and iodides at low pH can be oxidized by air oxygen to iodine. Both processes can be a source of titration errors. 

Iodine is very weakly soluble in the water and can be easily lost from the solution due to its volatility. However, in the presence of excess iodides, iodine creates I₃⁻ ions. This lowers free iodine concentration and such solutions are stable enough to be used in lab practice.  Still, we should remember that their shelf life is relatively short (they should be kept tightly closed in dark brown bottles, and standardized every few weeks). Iodine solutions are prepared by dissolving elemental iodine directly in the iodide solution. Elemental iodine can be prepared very pure through sublimation, but because of its high volatility, it is difficult to weigh. Thus use of iodine as a standard substance, although possible, is not easy nor recommended. Iodine solutions can be easily normalized against arsenic (III) oxide (As₂O₃) or sodium thiosulfate solution. 

It is also possible to prepare iodine solutions by mixing potassium iodide with potassium iodate in the presence of strong acid: 

5I⁻ + IO₃⁻ + 6H⁺ → 3I₂ + 3H₂O 

Potassium iodate is a primary substance, so the solution prepared in this way can have exactly a known concentration. However, this approach is not cost-effective and in lab practice, it is much better to use iodate as a primary substance to standardize thiosulfate, and then standardize iodine solution against thiosulfate. 

Iodine in water solutions is usually colored strong enough so that its presence can be detected visually. However, close to the endpoint, when the iodine concentration is very low, its yellowish color is very pale and can be easily overlooked. Thus for endpoint detection starch solutions are used. 

Iodine gets adsorbed on the starch molecule surface and the product of adsorption has a strong, blue color. 

In the presence of small amounts of iodine, adsorption and desorption are fast and reversible. However, when the concentration of iodine is high, it gets bonded with starch relatively strong, and desorption becomes slow, which makes detection of the endpoint relatively difficult. Luckily high concentrations of iodine are easily visible, so if we are using thiosulfate to titrate a solution that initially contains high iodine concentration, we can titrate till the solution gets pale and add starch close to the endpoint. In the case of titration with iodine solution, we can add starch at the very beginning, as high iodine concentrations are not possible before we are long past the endpoint. 

At elevated temperatures, adsorption of the iodine on the starch surface decreases, so titrations should be done in the cold. 

Finally, it is worthy of noting that starch solutions, containing natural carbohydrates, have to be either prepared fresh, or conserved with an antibacterial agent like mercuric iodide HgI₂. 

The two most important solutions used in iodometric titrations are the solution of iodine and the solution of sodium thiosulfate. Both substances can be easily obtained in a pure form, but their other characteristics (volatility, hard controlling the amount of water of crystallization) make them difficult to use as a primary standard. 

It is also worth mentioning that both solutions are not quite stable and they cannot be stored for a prolonged period. Iodine can be lost from the solution due to its volatility, while thiosulfate slowly decomposes giving off elemental sulfur. The latter process is easily visible, as thiosulfate solutions become slightly cloudy with time. 

Iodine solution 

It is not difficult to prepare high purity iodine through sublimation, but due to its volatility, iodine is difficult to weigh accurately, as it tends to run away. To minimize losses it should be weighed in a closed weighing bottle. Iodine should be kept in closed bottles also because it is highly corrosive and its vapor can damage the delicate mechanism of analytical balance. 

Commonly used solutions are 0.05 M (0.1 normal). 

0.05 M iodine standardization against arsenic trioxide 

The chemical characteristics of arsenic trioxide As₂O₃ make it a good candidate for a standard substance in many potentiometric methods, however, because of its toxicity, it is used less and less frequently. 

Arsenic oxide is dissolved in sodium hydroxide, producing sodium arsenite, which is a good reducing agent. In iodometry it is quantitatively oxidized by iodine to arsenate: 

Na₃AsO₃ + I₂ + H₂O → Na₃AsO₄ + 2I⁻ + 2H⁺   

The direction of this reaction depends on pH – in acidic solutions As(V) can oxidize iodide to iodine. To guarantee the correct pH of the solution we will add a solution of sodium bicarbonate NaHCO₃. 

Interestingly, when using As₂O₃ as a standard substance in other types of redox titrations, we often add a small amount of iodide or iodate to speed up the reaction. For obvious reasons, in the case of iodometric titration, we do not have to. 

Procedure to follow: 

• Weigh exactly about 0.15-0.20 g of dry arsenic trioxide and transfer it to the Erlenmeyer flask.
• Add 10 ml of 1 M sodium hydroxide solution and dissolve the solid.
• Add a drop of phenolphthalein solution.
• Neutralize with 0.5 M sulfuric acid, adding several drops of excess acid after the solution loses its color.
• Add slowly (do not cause the solution to foam up) 50 ml of 2% NaHCO₃ solution.
• Add 5 ml of the starch solution.
• Titrate swirling the flask, until a blue color persists for 20 seconds. 

0.1 M thiosulfate standardization against potassium iodate 

Potassium iodate is not titrated directly, but after it is mixed with iodate in an acidic solution, it is a source of iodine: 

IO₃⁻ + 5I⁻ + 6H⁺ → 3I₂ + 3H₂O

This reaction needs the presence of acid. Low pH both helps air oxygen oxidize iodides to iodine and speed up thiosulfate decomposition. Both reactions are detrimental to standardization, but they can be ignored if the water is oxygen-free and titration does not take too long. 

Iodine solution is then titrated with thiosulfate: 

2S₂O₃²⁻ + I₂ → S₄O₆²⁻ + 2I⁻ 

Procedure to follow: 

• Weigh exactly about 0.10-0.15 g of dry potassium iodate and transfer it to the Erlenmeyer flask.
• Add 40 ml of freshly boiled distilled water
• Add 2 g of (iodate-free) potassium iodide.
• Add 10 ml of 1 M hydrochloric acid solution and swirl the solution.
• Titrate swirling the flask, until a pale yellow.
• Add 5 ml of the starch solution.
• Titrate swirling the flask, until the blue color disappears. 

0.1 M thiosulfate standardization against potassium dichromate 

Dichromate – which can be easily obtained in a very pure form – oxidizes iodides to iodine: 

Cr₂O₇ ²⁻ + 6I⁻ + 14H⁺ → 2Cr³⁺ + 3I₂   7H₂O 

Iodine solution is then titrated with thiosulfate: 

2S₂O₃²⁻ + I₂ → S₄O₆²⁻ + 2I⁻ 

The first reaction is not too fast, so after mixing reagents they should be left for 5 minutes.  Also, the final color is different from what we are usually seeing during iodometric titrations, as the solution contains trivalent, green chromium. 

Procedure to follow: 

• Pour 80 ml of freshly boiled, distilled water into the Erlenmeyer flask (or better – flask with a glass stopper).
• Add 2 g of (iodate-free) potassium iodide.
• Add 25 ml of 1 M hydrochloric acid solution and swirl the solution.
• Close the flask and left it in a dark place for 5 minutes.
• Titrate swirling the flask, until a yellow iodine tint is barely visible.
• Add 5 ml of the starch solution.
• Titrate swirling the flask, until the blue color disappears.

0.05 M iodine standardization against thiosulfate 

This procedure is one of the two based on the reaction of thiosulfate with iodine: 

2S₂O₃²⁻ + I₂ → S₄O₆²⁻ + 2I⁻ 

If we have an iodine solution of known concentration we can easily use it as a standard for thiosulfate solution standardization and vice versa. This is a common situation in lab practice. 

The only problem is the selection of the volume of the thiosulfate sample. If we use 50 ml burette, and both solutions are 0.1 N (that means 0.05 M solution of iodine and 0.1 M solution of thiosulfate), we should use 45 ml of thiosulfate – to make sure we use an as large volume of the iodine solution as possible to minimize effects of the volume reading error.  However, there are no single volume volumetric pipettes of 45 ml volume. The most logical approach is to use a 20 ml pipette and 25 ml burette. 

Procedure to follow: 

• Measure 20 ml of thiosulfate solution and transfer it to the Erlenmeyer flask.
• Add 5 ml of the starch solution.
• Titrate swirling the flask, until a blue color persists for 20 seconds. 

0.1 M thiosulfate standardization against iodine 

This is almost the same procedure we have described above, just titrant and titrated substances are switched. 

2S₂O₃²⁻ + I₂ → S₄O₆²⁻ + 2I⁻ 

Again, we have a problem with the selection of the volume of titrated sample, and again the most logical approach is to use a 20 ml pipette and 25 ml burette. 

The procedure to follow is also very similar, just the moment of adding the indicator is different and we titrate not till color appears, but till it disappears:

• Measure 20 ml of iodine solution and transfer it to the Erlenmeyer flask.
• Titrate swirling the flask, until a pale yellow.
• Add 5 ml of the starch solution.
• Titrate swirling the flask, until the blue color disappears.

Make sure you also check our other amazing Article on : Standardization of Ceric Ammonium Sulphate