The spreading coefficient can be observed by adding one liquid to the surface of another liquid. The supporting liquid for instance is designated with ‘II’ while the liquid is added to the top by ‘I’ since it initially forms a lens. There are two possibilities, first, the liquid can spread over the surface of the sublayer liquid, or second, the added liquid will contract into a small lens on the surface of the sublayer liquid. We can predict what will happen to the system by determining net loss in free energy. The spreading of liquid is controlled by surface tensions of pure immiscible liquids and interfacial tension between them.
The concept of work of cohesion and work of adhesion help to understand the spreading of one liquid on another and predict whether it would spread spontaneously or not. There exists a mathematical relationship, which can be used to forecast the outcome of the situation called a spreading coefficient, denoted by S.
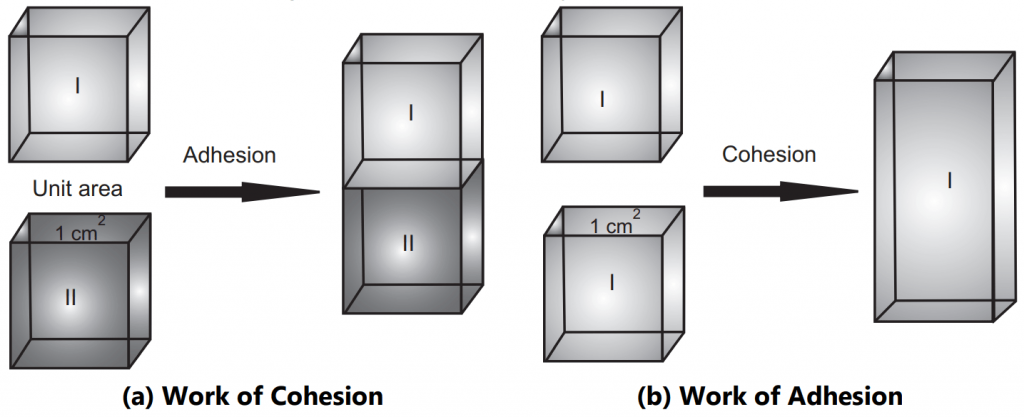
Work of Cohesion
Let’s consider a column of some liquid as shown in Fig.1(a), whose cross-sectional area is 1 cm2. On application of force to the liquid, it separates with the formation of two new surfaces each of 1 cm2 area. The work done in the separation of liquids is work of cohesion. It is defined, as a work required in separating the molecules of the spreading liquid so that it can flow over the sub-layer liquid. When the liquid alone is considered, no interfacial tension exists as cohesive forces are operating. Since two new surfaces are created the area becomes 2 cm2. The work of cohesion is denoted by Wc and is equal to surface tension times the amount of new area created. As per definition, the work of cohesion is written as;
Wc = 2γ1 … equation (1)
where γ1 is the surface tension of the liquid.
Work of Adhesion
Work of adhesion, Wa, is the work done to destroy the adhesion between unlike molecules. Let’s imagine the situation as shown in Fig.1 (b), where the column of liquid is made up of two immiscible liquids like oil and water. If a force is applied along the liquid column to cause the liquids to separate into two parts, the work done is work of adhesion. Hereby destroying the 1 cm2 interface between sublayer and spreading liquid we have created a 1 cm2 surface of sublayer liquid and 1 cm2 surface of spreading liquid. The work of adhesion is then expressed as;
W1 = γ1 + γ2 – γ12 … equation (2)
where γ1 is the surface tension of spreading liquid, γ2 is the surface tension of sub-layer liquid and γ12 is interfacial tension between them.
Spreading Coefficient
The spreading coefficient is obtained by the following equation
S = Wa – Wc … equation (3)
Substituting values from equation (1) and (2) we get
S = (γ1 + γ2 – γ12) − 2γ1 … equation (4)
The coefficient of each of the terms is one because we either created or destroyed 1 cm2 surface or interface respectively. On simplifying equation (4) we get
S = γ2 – γ1 – γ12
S = γ2 − (γ1 + γ12) … equation (5)
A positive value of S means that the liquid will spread and negative means it will not. Water has a surface tension of 72.8 dyne/cm, benzene has a surface tension of 28.9 dyne/cm, and interfacial tension between them is 35 dyne/cm. If benzene is added to the water surface, there exist two possibilities. First, the benzene can spread over the surface of the water if S is positive, or second, it will contract into a small lens on the surface of the water if S is negative. On substituting these values of surface and interfacial tension of water and benzene in equation (5),
S = 72.8 − (28.9 + 35)
S = 8.9
As the value of the spreading coefficient is positive benzene will spread on the surface of the water. In the spreading of organic liquids on the surface of the water, the initial spreading coefficient may be positive or negative, but the final spreading coefficient is negative. In addition to benzene to water, even though polar groups are absent in benzene, it spreads over the water due to stronger adhesive forces over the cohesive forces. With time benzene begins to saturate the water and the surface tension of water saturated with benzene decreases to 62.0 dyne/cm.
Now substituting values in equation (5) we get
S = 62.2 − (28.9 + 35)
S = −1.7
Since the value of S is negative, benzene contracts on the surface of the water and forms a lens. The spreading coefficient of substances depends on their structures, especially the presence of polar functional groups and non-polar carbon chain length. Polar substances such as acids and alcohols spread more freely compared to non-polar hydrocarbons like benzene, octane, and liquid petroleum due to the presence of polar groups.
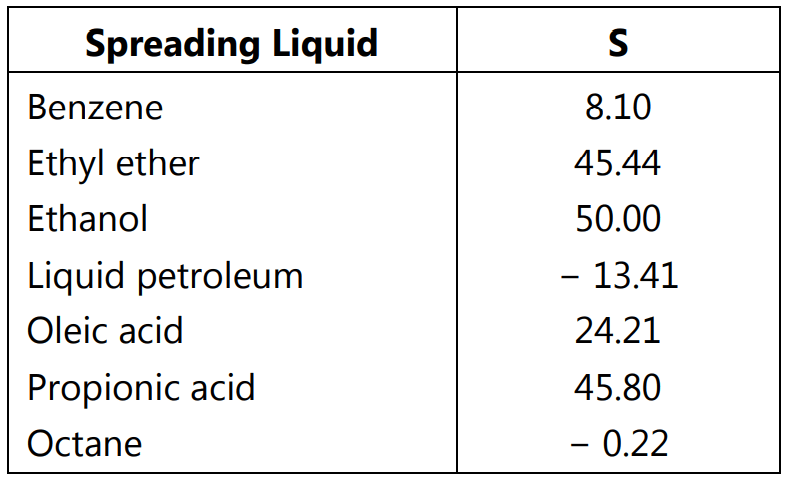
The phenomenon of spreading coefficient is useful in improving the bioavailability of drugs in dosage forms like creams and lotions by the addition of surfactant to increase polarity as well as spreadability. Spreading coefficient values of a blend of surfactants help to select the proper combination of the blend which improves the stability of emulsions. Spreading of liquid on a solid surface is also a useful tool in designing quality pharmaceutical suspension by improving wettability. Some values of spreading coefficients of liquids are listed in Table 1.
Example
At 20 °C the surface tension of water and chloroform are 72.75 and 27.10 dyne/cm, respectively while the interfacial tension between the two is 32.8 dyne/cm. Calculate (a) work of cohesion (b) work of adhesion and (c) the spreading coefficient of chloroform on water. Will chloroform spread on water?
Solution: (a) Work of cohesion
WC = γ1 + γ2 + γ12
= 27.10 + 72.75 − 32.8
= 99.85 – 32.8
= 67.05
(b) Work of adhesion
Wa = 2 γ1
= 2 × 27.10
= 54.20
(c) Spreading coefficient
S = γ2 – γ1 – γ12
= 72.75 – 27.10 – 32.8
= 12.85
Since the value of the spreading coefficient is positive, chloroform will spread on the surface of the water.
Make sure you also check our other amazing Article on : Measurement of Interfacial Tension
