The standard error of the regression is also known as the standard error of estimate(s). It is the measure of the variation of an observation made around the computed regression line. It represents the average distance that the observed values from the regression line. Smaller values of the standard error of regression indicate that the observations are closer to the regression line. If the standard error is ‘0’ that shows no variation corresponding to the computed line and the correlation is perfect. Standard deviation measures the variation in the set of data from its mean, likewise, the standard error of estimate also measures the variation in the actual values of Y from the predicted (computed) values of Y on the regression line. The standard error of the estimate is valid for linear as well as non-linear regression models. It is important in the calculation of confidence and prediction intervals.
The standard error of an estimate is calculated by the following formula:
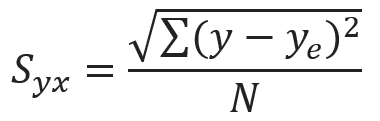
where,
- Syx = Standard error of estimate of y on x
- ye = Estimated value of y for a given value of x
Similarly,
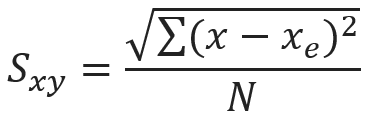
where,
- Sxy = Standard error of estimate of x on y
- xe = Estimated value of x for a given value of y
The large the value of Syx or Sxy the greater the scatter on the line of regression. In such a case the degree of correlation series is poor. The error of an estimate is an absolute measure and is given by the ratio S/σ. This ratio is also used for finding the value of the coefficient of correlation.

Make sure you also check our other amazing Article on : Application of Excel in Statistical Analysis
