Buffer Equation

Buffer Equation: Buffers have properties that the pH of buffer solution remains constant, does not change with the dilution, and on the addition of small quantities of acids or bases as well as on storage for long period.

In the case of moderate pH solutions addition of small amounts of acids or bases leads to absorption by buffer with only a slight pH change. For solutions having extreme pH values, small amounts of solutions of strong acids or bases for example, in the case of pH 1, acid concentration is relatively high (0.1 M) and a small addition of acid or base doesn’t change the pH of such solution significantly. In most cases, we need to know the pKa of the weak acid to do these calculations. The pH of the buffer solution can be obtained by rearranging the equation (1) for dissociation constant:

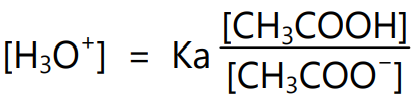
Since acetic acid ionizes very slightly, the concentration of acetic acid can be considered as the total concentration of acid in the solution. The term [CH₃COOH] can be replaced by the term [Acid] and the term [CH₃COO^– ] can also be replaced by [Salt]. Thus,

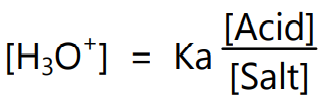
To calculate the pH of buffer solution containing both acid and its conjugate base the dissociation constant equation can be rearranged and rewritten as follows:

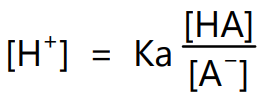
where [HA] is the concentration of acid and [A^–] is the concentration of its conjugate base. Expressing equation (3) in the logarithmic form it becomes,

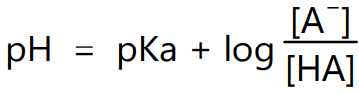
i.e.

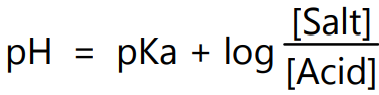
Equation (4) is called the Henderson-Hasselbalch equation. It can be used for pH calculation of solutions containing pair of acid and conjugate bases like HA/A^–, HA^– /A^2- or B⁺ /BOH.

The buffer equation for weak bases and their corresponding salts can be obtained like that of weak acid buffers. Thus,

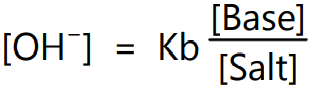
Since the ionic product of water (Kw) is H₃O⁺ × OH^–

OH^– = Kw/H₃O⁺ equation (6)

On substituting value for OH^– in equation (6) we get

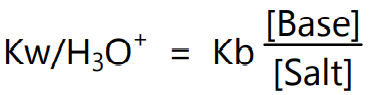
In logarithmic form equation (7) can be expressed as,

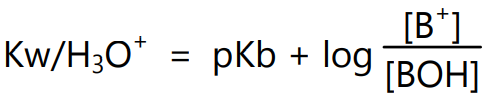
i.e.

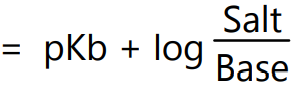
or

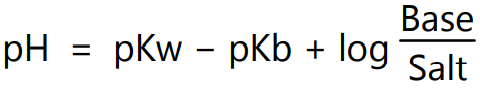
where, [salt], [acid] and [base] are the molar concentrations of salt, acid and base. Henderson-Hasselbalch equation is used mostly to calculate the pH of a solution prepared by mixing a known amount of acid and conjugate base. For example, the pH of a solution prepared by mixing reagents so that it contains 0.1 M of acetic acid and 0.05 M NaOH, the pH is calculated by using the Henderson-Hasselbalch equation. If half of the acid is neutralized, then the concentrations of acid and its conjugate base are identical. Thus quotient under logarithm is 1 which is equal to 0 and therefore, pH = pKa. Henderson-Hasselbalch equation is valid when it contains equilibrium concentrations of acid and conjugate base. In the case of solutions containing not so weak acids (or not so weak bases) equilibrium concentrations can be far from concentrations of components added into the solution. If acetic acid is replaced with dichloroacetic acid (pKa = 1.5) then the proper pH value is 1.78 because dichloroacetic acid is strong enough to dissociate on its own. Therefore, the equilibrium concentration of the conjugate base is not 0.05 M but is 0.0334 M.

It is important to remember that acids with pKa less than 2.5 dissociate too easily and the use of the Henderson-Hasselbalch equation for pH prediction can give wrong results, especially in the case of diluted solutions. For solutions above 10 mM and acids weaker than pKa ≥ 2.5, the Henderson-Hasselbalch equation gives results with acceptable error. The same holds for bases with pKb ≥ 2.5. However, the same equation works perfectly regardless of the pKa value in calculating the ratio of acid to conjugated base in the solution with known pH. Henderson-Hasselbalch equation also can be used for pH calculation of polyprotic acids, if the consecutive pKa values differ by at least 2. Thus it can be safely used in the case of phosphoric buffers but not in the case of citric acid buffers. The Henderson-Hasselbalch equation (also known as buffer equation) is adapted to consider acids and their conjugate bases leading to solutions that are resistant to pH change. This equation can be used for the following purposes.

1. To calculate the pH of a buffer solution when the HA/A^– ratio is known.

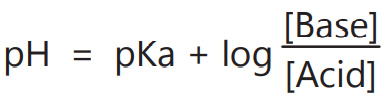
2. The pKa of various drugs can be determined from the pH of the solutions.

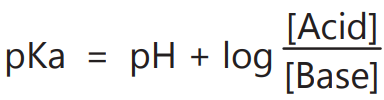
3. To calculate A^– /HA ratio to give a buffer of definite pH.

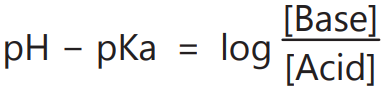
4. To calculate the HA/A^– ratio required to give a buffer of a definite pH.

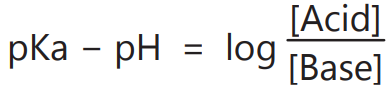
5. To calculate the pH changes due to the addition of an acid or base to a buffer solution.

6. To calculate the percentage of the drug ionized or unionized in the solution.

7. It is useful in the selection of suitable salt-forming substances.

8. It helps to predict pH-dependent solubility when intrinsic solubility and pKa are known.

Make sure you also check our other amazing Article on : Applications Of Buffers